轴承游隙与残余应力对轴承疲劳寿命的影响
滚动轴承是机械制造业中一种重要的基础零部件,对机械产品的性能、使用寿命等具有重要影响。经过多年发展,我国的轴承制造行业已经颇具规模,但高端轴承生产制造技术与发达国家之间还存在着较大的差距,轴承已成为我国大型关键装备制造业发展的制约因素之一。
GCr15作为最常用的轴承钢之一,广泛用于制造轴承套圈、滚动体及其他机械零部件。相关研究发现,在正确安装、润滑条件良好的情况下,轴承的疲劳破坏是滚动轴承的主要失效形式之一。
径向游隙是滚动轴承配合的一个重要技术参数,它的大小直接影响到轴承内部载荷在轴承圆周的分布状况,特别是影响滚动体最大载荷的变化,进而影响轴承的使用寿命、振动、噪声、摩擦、温升、旋转精度和刚性。
各种机械制造工艺(如热处理、切削等)的工件内会出现不同程度的残余应力(RS)。残余应力将会对材料的物理、力学性能产生巨大影响,工件表层残余应力是影响其结构强度与寿命的重要因素。因此,研究和检测材料中的残余应力对生产和科学实验都有非常重要的意义。
为了提高轴承的综合机械性能,需对轴承进行机械加工与热处理,在此过程中会出现不均匀的塑性变形以及不均匀的温度变化,内部会产生很大的残余应力,而轴承滚道表面的残余应力会直接影响耐磨性。Choi研究了加工残余应力对滚动接触疲劳的影响,结果表明,通过优化加工表面以下的残余应力分布,机械加工部件的滚动接触疲劳性能可以得到显著提高。Kanchanomai等研究了残余应力对碳氮共渗低碳钢疲劳失效的影响,结果表明,随着残余压应力的引入,碳氮共渗的AISI1015钢的疲劳抗力比未碳氮共渗的AISI1015钢的疲劳抗力要高。梁军帅等考虑套圈残余应力和滚道损伤对圆柱滚子轴承刚度特性的影响,发现硬化层厚度越大、硬化层残余应力峰值位置越深及峰值越大,则轴承的刚度越大。
综上所述,大多数研究都集中在游隙与接触关系以及机械加工与热处理对残余应力的影响,而较少将游隙与残余应力结合,进行更为深入的研究。因此,有必要针对深沟球轴承的游隙和残余应力对疲劳寿命的影响进行深入探究。
本研究采用有限元分析方法,探究与轴承疲劳寿命和主轴性能密切相关的轴承内部游隙的变化以及轴承滚道残余应力的分布,根据接触状态和残余应力的变化情况,研究轴承游隙和残余应力对轴承疲劳寿命的影响,为进一步研究深沟球轴承的疲劳寿命提供理论参考。
一、深沟球轴承力学分析与疲劳寿命计算模型
深沟球轴承的内圈承受主轴施加的径向载荷,并传递给滚动体,通过滚动体将内圈承受的载荷传递到外圈。其中的接触区包括内圈与滚动体的接触、滚动体与外圈的接触,深沟球轴承的失效为接触失效。采用的理论为赫兹接触理论,对于球轴承的接触区域是椭圆形的情况,最大压应力出现在几何中心,其大小为:
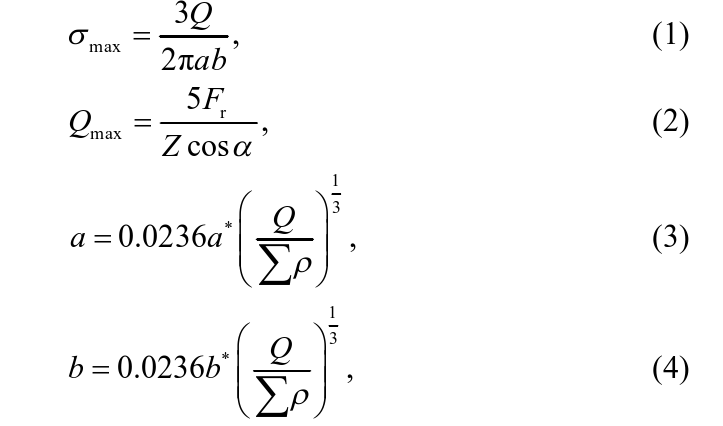
式中:Q为滚动体与滚道之间的法向力;a为接触区域的长半轴;b接触区域的短半轴;Fr为轴承径向载荷;Z为滚动轴承的滚动体数目;α为接触角;Σρ为曲率和函数;a*为接触椭圆量纲为1的长半轴;b*为接触椭圆量纲为1的短半轴。
为了分析深沟球轴承径向游隙及残余应力对疲劳寿命的影响,首先对轴承疲劳寿命的常用计算模型进行研究,从而对本研究的疲劳寿命模型进行修正。滚动轴承疲劳计算发展至今,众多经验和理论模型在各个领域均有应用,其中,经典L-P理论模型应用较为广泛。经典L-P模型假设位于表面下某处深度的最大正交剪应力导致裂纹的产生,进而主导轴承失效,其载荷寿命方程为:

点接触的向心球轴承旋转套圈内滚道的疲劳寿命为:

非旋转套圈外滚道的疲劳寿命为:

整套轴承的疲劳寿命为:

式中:Qc为滚道额定接触动载荷;Qci为内滚道额定动载荷;Qei为滚动轴承内圈当量滚动体载荷;Qco为外滚道额定动载荷;Qeo为滚动轴承外圈当量滚动体载荷;e为Weibull斜率,对于点接触 e=9/10,对于线接触 e=9/8。
二、残余应力的测定
轴承残余应力对疲劳性能的影响很大,而预先的表面形变强化通过在表层引入残余压应力,降低、抵消外载荷的不利影响,可使平均应力减小,大幅度提高疲劳强度和延长寿命。采用X射线衍射法(XRD)测定轴承表面残余应力,利用X射线穿透金属晶格时发生衍射的原理,测量轴承滚道的表面层由于晶格间距变化所产生的应变,从而测量轴承的残余应力。分别对6308碳氮共渗轴承内外圈沿圆周2点不同位置(图1)进行测定,测试数据见表1。

图1. 轴承套圈残余应力检测点示意
表1. 残余应力测试数据(MPa)
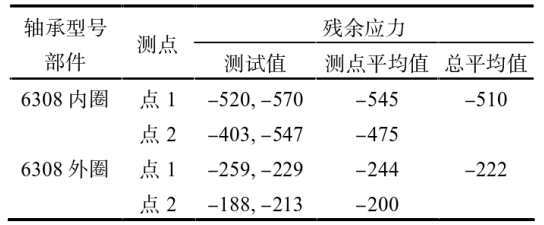
由检测结果可知,6308碳氮共渗轴承内外圈均存在残余压应力,其中,内圈压应力平均值为-510MPa,外圈压应力平均值为-222MPa。所测得残余应力为深沟球轴承的有限元仿真提供依据。
三、滚动轴承疲劳试验
由于轴承疲劳试验周期较长,本文做了4组试验。试验机通过液压方法对轴承施加径向载荷和轴向载荷,可通过调整不同重量的砝码来调节加载力,液压系统将砝码的重力放大一定的倍数施加在轴承上。试验机工装每次可装入4套轴承。本试验中只加径向载荷,大小为5kN。试验开始时,先调整转速到6000r·min⁻¹,轴承空转30min后开始逐渐加载,2h后加载到指定载荷。试验全程采用喷油润滑,通过温度传感器和振动传感器实时监测试验中的轴承温度和轴承振动信号。试验机每分钟保存一次试验数据。当温度或振动的均方根值超过设定上限时,试验机自动停机并保存试验累计时间和停机原因。拆机检查,确定停机原因。当发现轴承上有剥落时,确定轴承失效,并记录轴承寿命。
四、深沟球轴承有限元分析模型
4.1 几何模型的建立
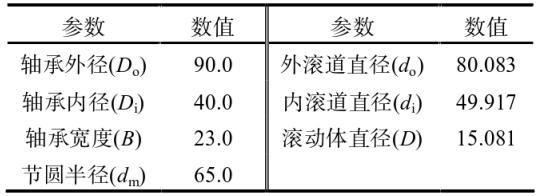
本文研究的深沟球轴承型号为6308,结构如图2所示,参数见表2。
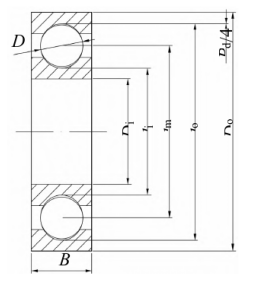
图2. 深沟球轴承结构示意
表2. 6308深沟球轴承尺寸参数(mm)
由于轴承的倒角及倒圆角的结构对计算结果影响很小,对接触分析基本无影响,因此为简化网格划分与计算,建模时将其忽略。深沟球轴承的保持架在整个过程中分离滚动体,使滚动体本身保持住或使其与一个套圈保持在一起,滚动体与保持架的摩擦力很小,对轴承疲劳寿命影响很小,因而不考虑轴承保持架的影响。基于SolidWorks进行自上而下整体建模,随后将模型导入有限元软件ABAQUS中进行网格处理,有限元接触分析对接触区网格划分要求非常高,如果对整个轴承做网格划分,那么求解会十分耗时,不利于模型修正与优化。因此,分别对轴承内外圈及滚动体接触区域的网格进行加密,使其结果尽可能精确,深沟球轴承三维模型如图3所示。
图3. 深沟球轴承三维模型
4.2 材料属性与接触特性设置
在ABAQUS中对轴承材料属性进行设置,本文研究的深沟球轴承内外圈及滚动体材料均为GCr15轴承钢,弹性模量为206GPa,泊松比为0.3,密度为7810kg·m-3,线膨胀系数为1.25×10-5℃-1。轴承内外圈滚道与滚动体接触类型为面面接触,根据凹面与凸面配对原则,即凸面为从面的原则,选择轴承内外圈滚道为主面,滚动体为从面,共创建生成8个接触对。设置接触对后检查接触面外法线方向,否则会出现过度穿透的问题。
4.3 边界条件与载荷施加
(1)在柱坐标系下对所有滚动体的轴向和周向自由度进行限制,只允许所有滚动体在径向发生平移,用于模拟内圈与保持架对滚珠的限制作用。
(2)约束轴承外圈表面所有自由度,用于模拟轴承装配时外圈固定的情况。保留内圈在Y方向的平移自由度,对其他方向自由度进行约束。
(3)残余应力场。通过调整温度参数来改变残余应力数据,轴承内外圈滚道接触区设置较高的温度(高于20℃),其他部分设置为20℃,从而得到轴承滚道残余压应力。为了便于分析,内外圈采用相同的残余应力分布,在此基础上施加径向载荷与约束条件研究深沟球轴承的受力情况。
(4)施加径向载荷。在轴承内圈内表面创建一个参考点,并将参考点与内圈内表面耦合,使参考点具有与内圈内表面相同的自由度。将集中力施加在参考点上,集中力方向垂直于轴承内圈内表面,从而获得轴承的径向载荷。
4.4 网格划分
将轴承内、外滚道划分为两个部分,分别在距离内圈滚道接触表面下2mm的位置划分出一部分。对滚动体与内外圈接触区进行网格加密,网格种子大小为0.1mm。与接触区相邻的部分网格种子采用非均匀分布,靠近接触区的位置网格种子逐渐密集,远离接触区的位置网格种子逐渐稀疏。
为降低计算成本,非接触区网格种子大小为2mm。考虑到单元格形状对分析结果影响较大,因此采用六面体结构划分网格,以提高分析精度与计算效率。模型网格类型为C3D8R,网格划分共产生295576个单元和345504个节点,模型网格划分后提交分析计算。
五、有限元分析与结果
有限元分析方法可以减少设计成本,缩短设计与分析的循环周期,减少试验次数,降低材料的消耗或成本。本文在有限元方法基础上开展试验研究,通过4组试验验证深沟球轴承的变化。轴承疲劳寿命受到材料特性、热处理、工作温度、几何尺寸和内部游隙等诸多因素的影响。其中,热处理引入的残余应力场与径向游隙对轴承疲劳寿命影响最为显著。通过调整不同单元间的温度参数,利用材料的热膨胀原理来模拟轴承热处理后的滚道残余压应力,分析得到的轴承滚道残余应力场云图及残余应力分布如图4所示。
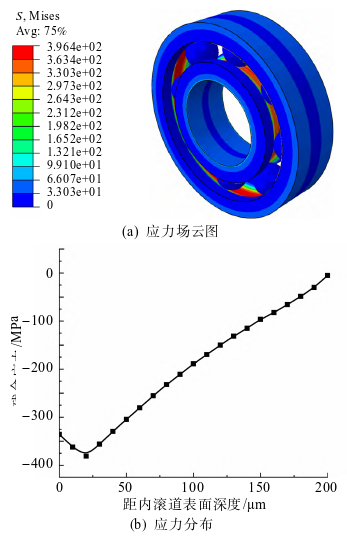
图4. 滚动轴承滚道残余应力场云图与应力分布
GCr15轴承钢热处理表面产生的残余应力为压应力,轴承内外圈滚道残余压应力随深度的增加呈先增大后减小的趋势,最后呈现残余拉应力。在深度为14μm处,残余压应力达到最大值,之后随着深度增加而逐渐减小,趋势与试验结果基本吻合。分析具有残余应力场的深沟球轴承在径向载荷作用下的接触力学性能,轴承内圈滚道等效应力大于轴承外圈等效应力,最大等效应力位于轴承内滚道表面以下,轴承内外圈接触应力云图结果如图5所示。
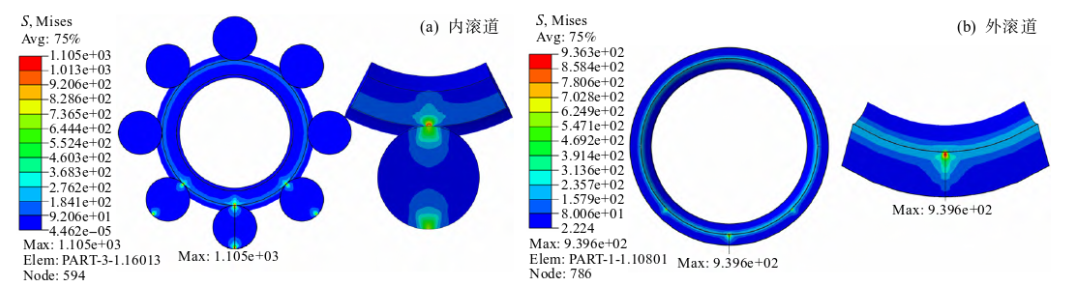
图5. 轴承接触应力云图
由图6可知,滚动轴承内滚道最大等效应力远高于轴承外滚道应力,且最大等效应力位于轴承内滚道表面以下0.25mm处,而球轴承疲劳剥落萌生于接触亚表面,这一结果与滚动轴承接触疲劳剥落理论相符。由图7可知,同一游隙下,随着轴承滚道残余压应力增大,最大接触应力逐渐减小,残余压应力与载荷相互叠加使接触压应力减小,有利于提高材料耐疲劳性能,从机理上验证了仿真结果的正确性。
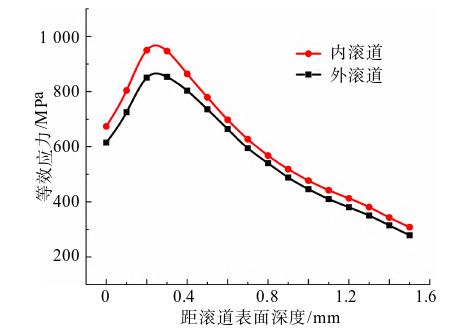
图6. 轴承等效应力与深度的关系
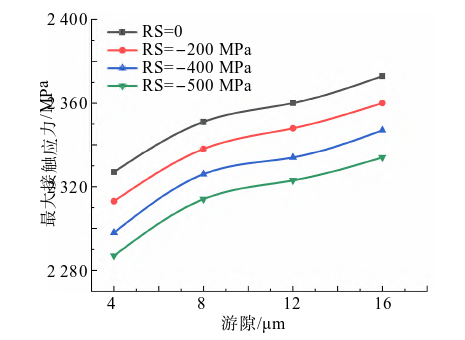
图7. 最大接触应力与游隙的关系
将有限元分析结果导入软件FE-SAFE中进行疲劳分析。轴承表面粗糙度选定为0.6μm<RA<1.6μm,采用Brown-Miller-Morrow疲劳模型对轴承内外圈进行分析。在轴承疲劳试验中,6308型深沟球轴承基本额定载荷为30.76kN,内部径向游隙值在0组区间范围内(6~20μm)。选择内圈残余应力-400MPa左右的4组深沟球轴承,将轴承游隙与残余应力综合考虑进行轴承疲劳寿命试验,轴承疲劳损伤往往发生在轴承内外圈滚道上,如图8所示。

图8. 滚动轴承内外圈疲劳剥落
轴承因接触疲劳在内圈出现点蚀坑而导致失效,疲劳寿命预测云图如图9所示。深沟球轴承内圈疲劳寿命与残余应力的关系如图10所示,试验中测得的轴承疲劳寿命要比预测结果大,这是因为P-L寿命计算理论是在不考虑润滑的情况下进行分析计算的,且随着轴承加工工艺的升级,轴承品质得到较大提升,因此预测结果相对较为保守。
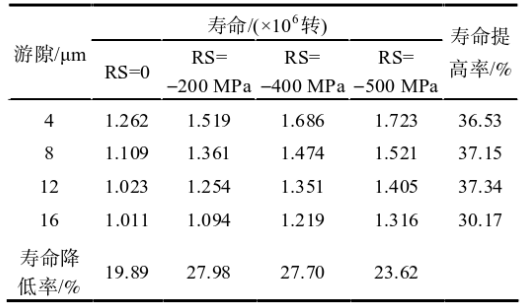
另外,疲劳寿命数据的分散性是疲劳载荷下所有结构和材料的共性特征,即在同一应力水平下, 疲劳寿命数据有明显的分散性。本文选取了平均寿命数据,滚动轴承疲劳预测结果见表3。当径向游隙一定时,随着残余压应力增大,接触疲劳寿命平均提高约35.30%;随着径向游隙的增大,残余应力引起的接触疲劳寿命增幅逐渐减小。由于随着游隙产生的应力增加而残余应力所占总应力的比例减小,增加轴承径向游隙将会降低疲劳寿命因残余应力产生的增幅。当残余应力一定时, 随着游隙的增大,接触区滚动体数减少使滚动体与轴承内外圈接触面积减小,轴承接触区最大应力随之增大,进而导致轴承疲劳寿命平均降低了24.80%,轴承内圈疲劳寿命远高于轴承外圈寿命。将模拟结果与试验结果对比,发现仿真与试验结果误差在16%的工程允许范围内,进一步验证了接触模型的合理性。

图9. 轴承疲劳预测云图
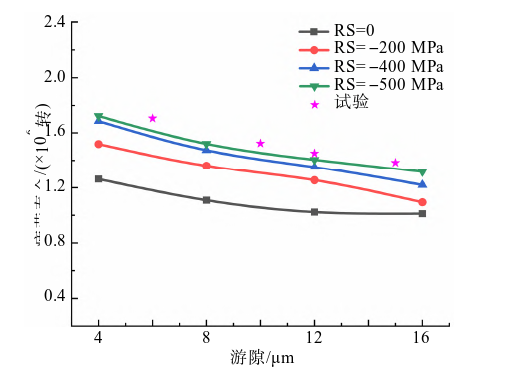
图10. 深沟球轴承内圈疲劳寿命与残余应力的关系
表3. 滚动轴承疲劳预测结果
六、结论
(1)当残余应力一定时,随着游隙的增大、内外圈滚动体数目的减少,轴承接触区最大应力增大,从而导致轴承疲劳寿命平均降低了24.80%,轴承内圈疲劳寿命远高于轴承外圈疲劳寿命。
(2)当轴承游隙一定时,残余压应力从0增加到500MPa,部分抵消了径向载荷所产生的不利影响,可使平均应力减小,从而使得轴承寿命平均增加了35.30%。随着游隙的增大,残余应力引起的接触疲劳寿命增幅逐渐减小。




